
254
cumpridos para se manter a classificação obtida, limitando características de propriedades térmicas e
estabelecendo regras que privilegiam ventilação natural e iluminação natural.
Os limites das classificações para as situações de resfriamento e de aquecimento são expressos,
para cada Zona Bioclimática, em graus hora de resfriamento (GH
R
)
14
e consumo relativo para
aquecimento (C
A
) (kWh/m
2
.ano), respectivamente. As tabelas 3 e 4 são exemplos dos limites das
classificações para a Zona Bioclimática 4.
Tabela 3.
Zona Bioclimática 4
Classificação para a condição de verão
Tabela 4.
Zona Bioclimática 4
Classificação para a condição de inverno
Eficiência EqNumEnvAmb
Resfr
Condição
Eficiência EqNumEnvAmb
A
Condição
A
5
GH
R
≤727
A
5
C
A
≤5,838
B
4
727<GH
R
≤1453
B
4
5,838<C
A
≤11,675
C
3
1453<GH
R
≤2180
C
3
11,675<C
A
≤17,513
D
2
2180<GH
R
≤2906
D
2
17,513<C
A
≤23,350
E
1
GH
R
>2906
E
1
C
A
>23,350
Fonte: Brasil (2012) Fonte: Brasil (2012)
3.3 Conjuntos
Crisp
vs.
conjuntos
Fuzzy
Analisando as classificações das envoltórias das edificações, tanto residenciais quanto
comerciais, percebe-se imediatamente que os limites entre as classificações consecutivas são
definidos por valores unitários específicos e limítrofes. A variação de uma unidade dos valores de
referência das classificações pode ser o suficiente para que uma envoltória receba a classificação
no nível seguinte, com maior ou com menor grau de eficiência. Estes conjuntos de valores de
referência pertencentes a cada uma das classificações de eficiência energética são representados
pela teoria tradicional de conjuntos
Crisp
.
Na lógica
Crisp
um determinado elemento pertence única e exclusivamente a um determinado
conjunto correspondente. Essa teoria trabalha com sistemas lógicos binários, onde o conceito verdade
é absoluto e os valores verdadeiro (1) ou falso (0) são as únicas correspondências a este conceito.
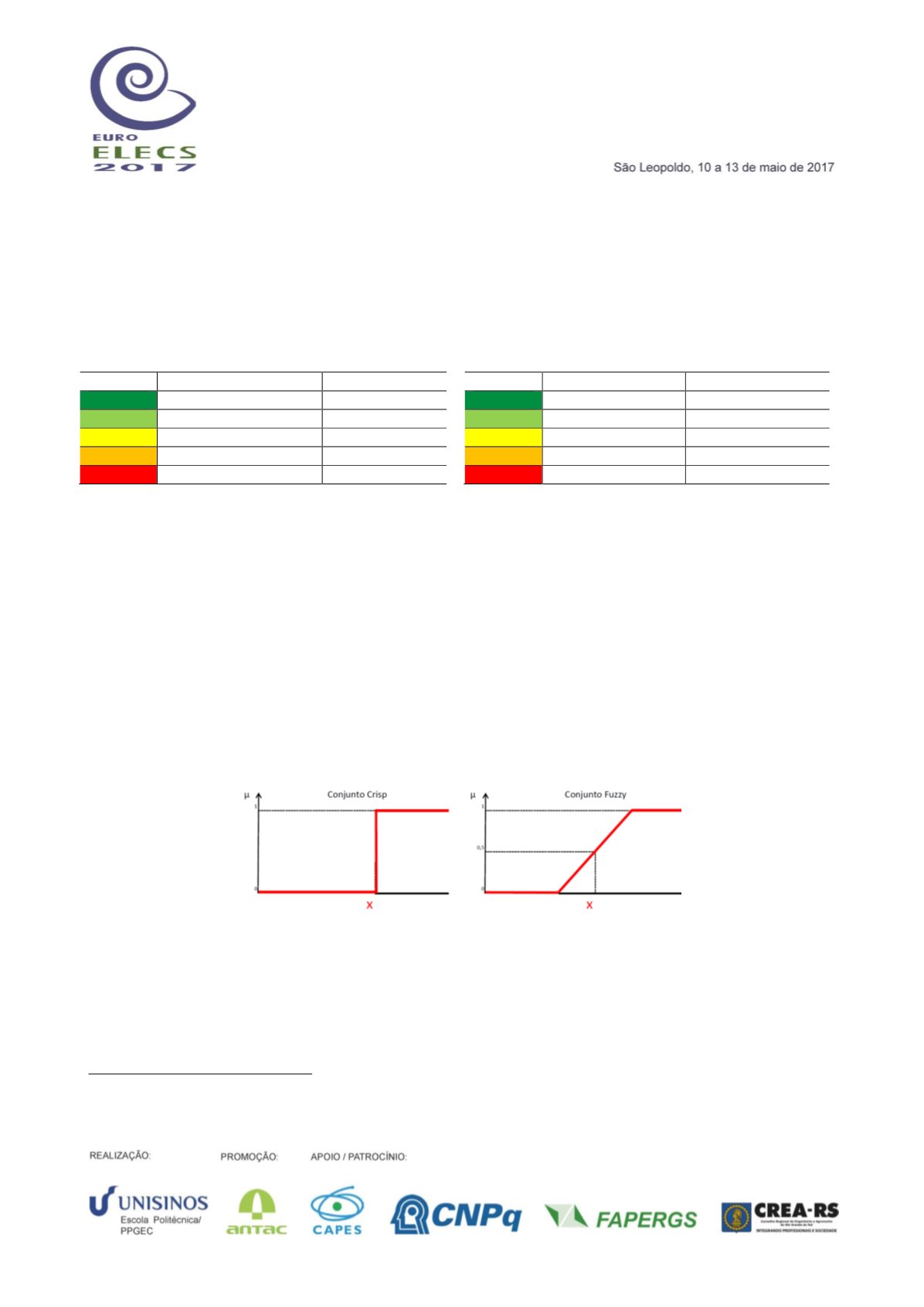
Figura 4.
Representação gráfica dos conjuntos
Crisp
e
Fuzzy
A lógica
Fuzzy
(Nebulosa) trabalha com linhas de raciocínio que substituem o exato pelo
aproximado (TANAKA, 1996). Na teoria dos conjuntos
Fuzzy
um elemento
x
pode pertencer a um
determinado conjunto
M
e também a um outro conjunto
N
. Por exemplo, se trabalharmos com a
variável linguística
idade
e com os termos linguísticos
jovem
e
adulto
, é correto afirmar que um
homem de 30 anos já é adulto, mas ainda é jovem. Basta classificar o grau de pertinência (µ) deste
homem a cada um dos conjuntos correspondentes. O grau de pertinência (µ) é uma grandeza
14
GHR: Graus-hora de resfriamento, unidade na qual são produzidas as respostas na equação de EqNunEnv
Resfr
,
significando o somatório da diferença entre a temperatura operativa horária e a temperatura de base, quando a primeira
está acima da segunda, no caso de esfriamento, adotando a temperatura de base como 26° C (BRASIL, 2012).
Fonte: Edição dos autores a partir de Tanaka (1996)


















